So you want to measure the muzzle velocity of a cannon.
The instructions here will let you figure it out.
To make it somewhat less hazardous we will be using a bean shooter as our cannon.
Print out the form you find here. You will be filling in your data on the form and using the tables on it to calculate the projectile's velocity.
And print the large protractor quadrant you find here to use to measure the angle when you get to that part of the experiment.
You will need a projectile to shoot. Navy beans work well. Later you will need to know the weight of your projectile. If your scale isn't sensitive enough to weigh one bean count out enough to weigh on your scale and then divide by the number of beans to get their average weight. If you are selective and don't include very small or very large ones you will get a more accurate result. Record the weight of one bean in the first box in the "Projectile mass" column.
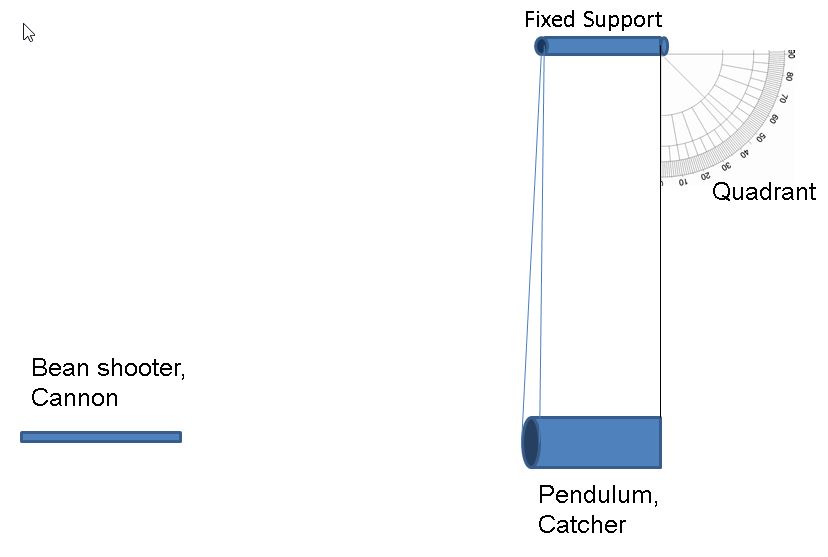
Next the "cannon". A straw that is large enough for the bean to slide through easily. We found some very long ones that I am told you will get when you order a Bahama Mama in some establishments. A wire through the straw near one end you will blow through will turn the straw into a muzzle loader. That will make it less likely to accidentally fire the bean into your uvula (look it up).
Now we need something to catch the projectile. We use a single sheet of paper rolled into a tube that is closed on one end. Since the bean must stay in the tube we have found that it works better if you crumple the paper and flatten it some before you form the tube. That way the bean is more likely to be caught and not bounce out.
We also need the weight of the pendulum, so you should weigh it now and record it on the data sheet in the first box in the column labeled "Pendulum mass". You can divide and put the result in the "Ratio" column.
The catcher now becomes the bob of a pendulum. By hanging it on three threads you can make sure it is level, in line with the cannon, and will swing in a straight line. The tables that you will be using to determine the muzzle velocity of the cannon are based on a1.00 meter length of the pendulum, from the support point to the center of mass of the pendulum bob.
Now you need a way to measure how much the pendulum is deflected when it catches the projectile. Print out the protractor quadrant and fasten it so the circle on the quadrant is close to the pendulum support point for one of the threads and the 0 degree mark and the pendulum will swing in front of it.
It is a good idea to color that thread so that it is easy to recognize when the pendulum is moving.
Here is a diagram showing how everything should look.
Now we are almost ready to shoot. EVERYONE PUT ON YOUR SAFETY GLASSES.
Position your marksman far enough away so the air from the straw doesn't move the pendulum very much but close enough that she/he can hit the open end of the pendulum (at least sometimes).
Position the observer so he/she can see the thread in front of the quadrant with it in line with the 0 degree mark.
If everyone is ready, FIRE!
The observer should record in column titled "Measured angle A" the angle that the pendulums swings to when it catches the bean.
Repeat several times recording each result in the boxes in that column.
We now have everything we need to figure out the velocity of the projectile (bean). Here is how it will work. When the bean hits the pendulum its momentum is shared with the pendulum giving it some kinetic energy. The pendulum swings and because of that it rises. So its kinetic energy is converted to potential energy. It will stop when all of its kinetic energy is converted to potential energy. That will happen at the greatest height (angle). Since you recorded the angle you have a measure of the momentum and since you measured the weight you have everything you need to get the velocity of the bean.
Now go the the tables on the data sheet. They have been set up so that the calculations outlined above are all taken care of for you. First, Look up (
